 Joseph Fourier, French mathematician (1768-1830) is one of my heroes. Join me back in 1994 during a lonely nightshift in the control room of the LEAR antiproton decelerator at CERN.
Joseph Fourier, French mathematician (1768-1830) is one of my heroes. Join me back in 1994 during a lonely nightshift in the control room of the LEAR antiproton decelerator at CERN.
The walls are made from stacked computer racks and other equipment. Indicator lights flash quietly; cooling fans whir and oscilloscopes scan traces across the screens, showing the heartbeat of the particle accelerator. “AIW” I write in the paper log book, All Is Well.

On the eternally long and lonely nights, we – a small team of operators – kept CERN’s accelerators running. Most of the operations are automated and except for the occasional intervention or dealing with equipment breakdown, the nights leave a lot of spare time. We can’t sleep and have to stay alert and so, most of us turn to programming: developing software to automate our jobs even further.
At that time I was developing software that controlled the Ultra Slow Extraction of antiprotons (most expensive material known to man: 100 MUSD for 1 microgram!) from the accelerator. LEAR was designed as a “storage ring” that kept the antiprotons in orbit and an electrostatic knife would peal the beam of antiprotons slowly and send them to the detectors of groups of sleepy physicists, dreaming of Nobel prizes.
This process is governed by the Diffusion Equation. This equation was formulated by Joseph Fourier is also referred to as the Heat Equation, as he was trying to understand how heat diffuses through steel. To put it simply: if you put a metal rod in the fire, how long will it take before it gets to hot to hold on to?

Although the equation is short (I won’t show it to avoid math alerts going off and scare you away), it is very hard to solve. Joseph Fourier did something amazing to solve it: he invented a new type of analysis. The amazing part is its beauty and universal importance: without it we would not have had radio, TV, mobile phones etc. It is the first thing every engineer learns when starting a degree course. But Fourier never knew that as it happened long after he died. He invented it to analyze heat.
Under the fluorescent lighting of the LEAR control room, this Diffusion Equation occupied me. This equation governs more than heat or antiproton beam extraction: it is a formula for natural decay of things. For example when you build a sand castle on the beach, after a short while it will start collapsing. Perhaps it dried out or perhaps a wave came over it but within hours, you will have a blobby mound of sand left over. That is diffusion too. As is the decay and collapse of any man made structure over time in absence of maintenance.

So, I thought, if the diffusion equation tells us how things collapse, what would happen if we turn it around? What if we start with a blobby mound of sand and we let the inverted equation lose at that, would we get a sandcastle? During those night shifts I wrote software to simulate this and using a numerical approach, I managed to conjure sand castles out of blobby mounds.
So what? Geeky stuff for tired operators, or what!?
Not so fast… By creating sand castles out of blobby mounds using an inverted diffusion equation, I had created a new mathematical beast: the Creation Equation.
Imagine that: an equation that creates things out of formless blobs; a world out of nothing: the holy grail of science!!!
However … I had a problem. Although my night shift experimentation worked well enough using computer simulations, I never managed to actually invert the diffusion equation using mathematics. I used numerical approximation on a computer instead. As beautiful as Fourier’s solution was, it wasn’t suitable for inverting the diffusion equation.
That was 1994 and to this day, 20 years later, I occasionally wake up wondering when I’m going to solve the riddle of the inverting the Diffusion Equation.
—–
It’s strange how such personal challenges can drive us. It can push us into a life time of searching. So it is with the Creation Equation. There is a sequel. On the surface it is quite unrelated and it has nothing to do with Fourier’s equations.
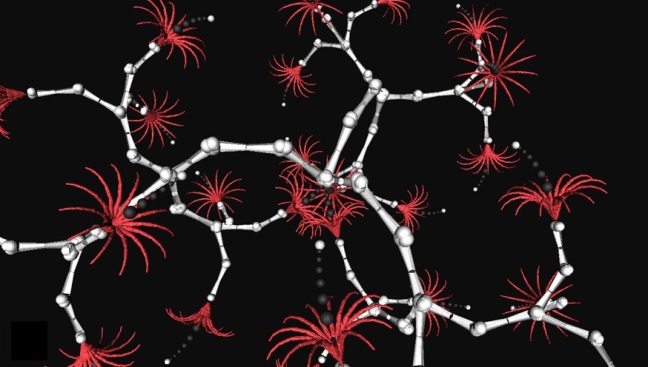
As some of you know, a few years ago I “discovered” genetic fractals. You can see them in the pretty pictures I plaster all over this blog. But there is also a mathematical theory behind that.

A short while ago, after trying for 3 years, I finally found a proper formulation for these genetic fractals. An equation, if you like. This equation describes how things grow and evolve in nature. It is driven by a mathematical formulation of DNA and depending on that DNA the formula will generate trees, flowers, kidneys or any other natural form, or unnatural form for that matter.
Now, you may not be into maths or perhaps even dislike it. The amazing thing about maths is how much news and information can be packed into a few symbols. Mathematicians read these equations like books and draw out the most surprising rabbits.
For example, using this genetic fractal equation with the approximate DNA for a tree, you can study what happens when the tree matures. The animation below shows that. You can also see what happens if the branches were to grow further. It can grow fruit etc.
This too is a Creation Equation: it creates life forms from DNA. But here is the cracker: I can invert this equation. I can reverse time and see the opposite of growth: see the tree shrink back to its origins. Where was the tree before it grew its first branch, i.e. a small green trunk?
From experience we know the answer: an oak tree comes from an acorn. So will this Creation Equation show that?
Sadly, my Creation Equation didn’t give that answer. It gave a very strange answer that bothered me for a while. A tree, it said, doesn’t come from a seed; instead it comes from another tree. The Creation Equation tells me that a tree is in fact a branch of a much bigger tree.
Upon reflection, this is the perfect answer! A tree is itself a branch of its parent which is itself a branch of its parent etc. However, because trees couldn’t grow infinitely large, occasionally the ends of branches, packed with nutrients in the shape of an acorn, drop onto the ground and continue growing there.
That’s an amazing perspective. Every tree of a species is truly and out growth of its earliest predecessor. There is only one tree that happens to have fallen apart into billions separate branches across the world.
That’s what this Creation Equation tells us.

By extension it also tells me that every living species not only has a single common ancestor, in fact, every living being is part of that same organism whose root is that common ancestor. “We are one” is not just New Age speak: we really are one.
But we knew this already, right?
That often happens in science, we discover equations that match what we know already. It tells us scientists that we are on the right path. The next step is to look back further. What preceded the first common ancestor? The science of evolution tells us that it all started with a hot cocktail of monomers of life: Amino acids, Phospholipids and Nucleotides. How exactly this soup merged into life, has not been fully understood. And that is an understatement.

I wonder what my Creation Equation has to say about that? One thing I can already see and that it wasn’t a random event. It is pointing at a single point of origin, a true singularity.
When I figure that one out, I promise to update you.
(Another understatement)
PS: in case you wonder – the Creation Equation is not a metaphor, here it is (in its 2-dimensional form).
It includes Euler’s “God Equation”, as it should 😉 The key lies in the DNA formulation, D which is a multi-valued function. I know this doesn’t tell you much but I’m sure to publish this properly somewhere, some time.

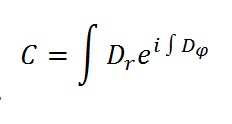
Mind smiling.
Now, if there is a creation equation (wouldn’t that be something!) it must allow for mutations and adaptation. How does this play out?
The creation equation loves mutations. Just punch the DNA function a little and it mutates the thing it creates.
Since mutation is the mother of adaptation, Bob’s your uncle 🙂
Ta-da!
What are your outside parameters to guide it? I forgot what they were exactly, but John Conway’s Life game had four, if i remember correctly.
Yes, he had 4.
The Creation Equation has as many as you like.
If you don’t tell it how to react to its environment it will happily grow forever. If you tell it to watch out for cars and skinheads then it will do so. You can tell it about limitations of space, climate, food supplies etc.
In maths we call these “boundary conditions”. You are right to mention it: it is these boundary conditions that make this (and any) equation interesting.
I’m seriously unschooled in science, but a creation equation requires negative entropy, yes? I think that implies that the greatest complexity, and I’m sure there’s a better word for it than complexity, is always now. Now tapers off to no potential in all directions. Complicated.
Interesting yoiu should describe it like this.
The first equation I mentioned, the Diffusion Equation by Joseph Fourier was indeed an equation of entropy: the decay of things. Its inverse would be negative entropy indeed.
Alas, search as I did, I haven’t made that one work yet. But I haven’t given up hope.
The equation I wrote myself, the Creation Equation also shows this ever increasing complexity in the now. As time marches on, it creates a more and more complex world. Why? Because there is no stopping it.
Looking back in time, through the looking glass of the Creation Equation, it seems that that complexity diminishes and the complexity of now becomes the simplicity of that first moment when it all started.
That first point is my quarry and I’m breathing down its neck…
I’ll be honest, I’ve had a lifelong math phobia. And yet every time I read one of your posts I’m entranced. Not only do you write so intriguingly about your subject, you also make the world of math and science sound so . . . magical, for want of a better word. Thank you!
Many math teachers believe that their job is to explain maths and get students to find the right answers. If only they would approach maths like a painter approaches a painting. Even the most basic equation is a gateway to tremendous beauty and mystique. Even 1+1=2 hides treasures that no one has found as yet. Who cares if the answer is right?
I found maths hard at school and didn’t enjoy it. When studying engineering, I loathed it. But when I ended up taking a full degree in maths,with the OU something strange happened. The people teaching were passionate. They couldn’t wait to point at the beauty and mystery of maths. They told tales of mathematicians long gone. About their love affairs, there fights and their genius and madness. They took maths off the page and showed us what it is: a world so big that it begs us to enter. An Aladdin’s cave of gold and diamonds, if only you could work out the password.
I’m delighted you can read around the maths and hear the story behind it. Made my day, you did 🙂
I like your approach to maths, and agree completely that it is often taught in a very poor and uninteresting way. Which may be why I never learnt much of it.
If you are trying to get all the way back to the initial singularity, would this mean that you need to get all the way back to the foundations of mathematics? That is,. as you approach the initial condition for your equation are you going to come up against problems related to the continuum, Russell’s paradox etc?
Good observations Guy. I expect that the singularity of life comes after the foundations of mathematics so they won’t get in the way. The Creation Equation can’t go much beyond that. It is based on the notion of cause and effect and once you get to the next singularity, i.e. the origin of reality and the universe the foundations of maths don’t exist yet.
I have some thoughts about the origin of cause and effect chain which can only start if the cause of the first cause is that cause itself. What this means is that if the Creation Equation survives that long, chances are that it is in fact a solution of a more fundamental equation. That more fundamental equation would have to have be able to generate itself in order to be its own cause.
Russel’s Paradox (and others) won’t be an issue. I’m quite certain that such paradoxes are result from human defined logic which has its limitations. Even cause and effect falls into that category which are rooted in duality.
I wrote a few posts on that subject: spectrum of duality, Fractal Reality and Your Anti-Cartesian Life
But … I really don’t have all the answer – if any! However, I’m having great fun in looking for them 🙂
How does this creation equation relate to the heat diffusion equation exactly? I know how to solve the latter – using numerical simulations or Greens functions (that “dissolving peak of heat” function…) – but here I’m lost.
The exponential function with the integral reminds me of path integrals in physics, but probably only because capital D is used a shorthand for an operator in quantum theory.
The diffusion equation is unrelated to the creation equation. I used it as an example of an equation that creates order out of chaos, which is what the inverse (w.r.t. time) of the diffusion equation does. I also used numerical analysis to solve it.
The D in the Creation Equation refers to “driver function” and I colloquially refer to it as DNA because it looks similar both in function as in aspect.
These are indeed path integrals. The paths are the branches of the tree (or other organism). The driver function is multi-valued (like the square root of a variable has two solutions, not one). Every time an additional value appears, the paths will branch into a new direction.
No idea if that relates to quantum theory, but I doubt it 🙂
Fourier analysis is really fascinating, and the idea of going in reverse is really, really cool. I know you expounded a bit on your creation formula in your responses, but I’d love it if you could blog on that in detail, including some details on the program you wrote to implement it — or an approximation to it.
One thing I had wondered about was this… if everything has a wave function (is this true?), and Fourier analysis can decompose waves into a sin/cos expression, then reality can be represented by (a hideously complex) sin/cos expression. Maybe it’s not useful, but the idea is nifty 🙂
Hi Bloggingisaresponsibility, great to hear from you!
The Fourier equation I tried to reverse before was the Fourier’s diffusion equation, not his Fourier Transform that involves sin/cos .
Having said that, if you look at the Creation Equation that I developed, it does include Eulers exponentional formula for a … sin/cos expression. Indeed, the organic forms that this Creation Equation generates is an expanding network of waves that intersection and split, combining into organic forms that we are used to.
Surprisingly, formulation is not hideously complex at all. However, when you let it evolve for a while, what it creates is very complex.
I am currently developing software that uses this Creation Formula as the basis for a design tool. More here: http://www.geneticfractals.com/index.php
However, I will blog more about the Creation Formula itself. It has some amazing properties and I can’t wait to share!
Thanks for the clarification. I had read of the Fourier Transform in the context of heat diffusion, so when I read your post, I went from diffusion to transform. My apologies.
Checking out your site. Thanks for the link, and I’m eagerly awaiting your blog on the Creation Formula!
Fascinating stuff. You say, GF, that as you track backwards the equation approaches the simplicity of the initial singularity and focuses more and more narrowly on the ‘Now’. Would it not also be true that this simplicity appears if you simply focus on the ‘Now’ regardless of whether this ‘Now’ it is in the past or the present?
If the equation takes us back the a singularity then I wonder about its relationship to the equation or procedure used by G.S. Brown in ‘Laws of Form’ to describe the origin and development of form and complexity. Seems to me there ought to be a connection.
I would disagree with the idea that ‘the singularity of life comes after the foundations of mathematics’, and cannot really make sense of it. I would rather say that the division of the singularity in or by consciousness (iow the birth of intentional consciousness) actually IS the foundations of mathematics. This is the view expressed by Weyl in his book on the continuum., if I understand him correctly, and by Brown.
Pardon me if these comments are wide of the mark. I’m no mathematician, just fascinated by the connection between foundational maths and metaphysics.
Yes, now is as good starting point as the past – I suspect that a singularity of creation is happening all the time. It isn’t so much going back in time as it is following the path of life to a beginning. A single daisy living in the now should be able to tell that story.
I don’t know G.S. Brown’s work, thought it seems intriguing. I try to find formulations that avoid dualities. Instead I seek continuous forms where the entire spectrum between form and no-form is covered. This would seem to connect with Weyl’s continuum – which I don’t know either 😦
Although the formulation of mathematics must necessarily come after conscious awareness, which would suggest it follows the singularity of life, in my view, the reality that mathematics can describe goes back to the birth of reality, before conscious awareness. However, it may well be that the singularity of life, reality and consciousness is one and the same thing.
I am of course hugely intrigued about the foundation of mathematics and more than anything, I’d like to figure where the most fundamental notion comes from: the equation sign (and its siblings >, < etc). In my view the equation concept is one of the first dualities (it separates two things by defining their relationship) and it is therefore a human concept. However, to imagine mathematics without it is quite hard, but not impossible. If anything, the equation concept can also seen as a symbol of creation (something becomes something) and from that perspective, the singularity of maths – and the rest – may well be hiding exactly there.
I can agree with your first para. above, and it seems an important point. The ‘Now’ is always ‘Now’.
I can’t be sure you’ll like them, but I feel that Brown and Weyl are completely wonderful on the emergence of mathematics from the singularity. Brown does it by a process of distinction-making, and this sounds very like what you’re doing. His method avoids Russell’s paradox and can therefore be fundamental.
Weyl comes at it from a different angle. He points out that the continuum of physics and mathematics (and naive perception) is not the continuum that is presented to us in experience and intuition. The former is extended as a series of points, moments, durations, locations etc., while the latter is entirely free of such things. Thus Weyl’s intuitive (and real) continuum would be the (ever-present) singularity, while the extended (unreal) continuum of mathematics and physics would be emergent as a creation of our reason, a theory-laden interpretation of experience. This would be consistent with Brown’s ‘calculus of indications’.
I like to promote Brown wherever possible, and Weyl’s book on the continuum seems an excellent accompaniment. Weyl’s view seems a thousand times more sophisticated than that of the average physicist, and not insignificantly allows the possibility that Buddhist doctrine might be true.
It would, however, depend on the idea that consciousness is present from the beginning, and is in fact the explanation of the beginning. In this way Brown and Weyl become consistent with the Buddha and Lao Tsu on the emergence of number and form.
Sorry if this is OT. It is one of my hobby-horses.
What do you mean by ‘the singularity of life’? Do you mean the first occurrence of biological life?
You intrigue me – so I have to read more about this. The Wikipedia entries are not brilliant. Do you have pointers at intorductions to Weyl and Brown?
Yes, I mean the transition from inanimate matter to biological life. Biological life is not all that well defined but their must be an evolution from inorganic chemistry of dead matter (rocks, gas etc) to a biological mechanism that sustains itself in certain environments.
Talk about OT hobbies!
Yes. Life or death issues though.
The relevance of what you’re doing with mathematics to metaphysics and also to mysticism seems immediate. Implausible maybe, but Brown discovered the mathematics of creation, as described, he later discovered, by Lao Tsu, while designing electric switching circuits for a railway company.
Life had a singular start on Earth, but did consciousness? Consciousness would have to emerge prior to biological life if we are ever to reconcile evolutionary theory with religion, so it is an important issue.
If you visit my blog you’ll see a page marked ‘links’. There is a list of pages discussing Brown’s work. There should also be a link to a brilliant essay about Weyl and the continuum by someone whose name I’ve forgotten for the moment.
Weyl’s book is mostly maths and so mostly beyond me, but there is one passage that clearly explains his view of the relationship between the continuum of mathematics and the ‘intuitive’ continuum, the umanifest continuum of unmediated awareness. It is brilliant and makes some crucial observations, and I intend to put it up as post sometime soon.
. .
Brilliant, this is great. I started reading Spencer Brown and Weyl and am hooked. These are exactly the sort of questions I ask myself. For a long time I have been trying to understand Lao Tsu and to some degree, I do. However, it remains highly philosophical and it is great to see mathematical formulations of those thoughts.
I am a great believer in experience and most of what I know about Lao Tsu and consciousness is really from experiencing it,i.e. get away from symbols and computers and go outside to experience space and non-space.
I’ve got a lot of catching up to from your blog. Thanks for the great pointers!
Incidentally, I was an electronics engineer before I became a mathematician. Hence, I warm to Brown with great ease.
Great stuff. I think mathematicians may have an advantage when delving into these issues, since they are used to the kind of abstract thinking and logical analysis required. They also tend to be ruthless at philosophical logic-chopping, where many people allow emotion and personal preferences to muddle the issues.
My maths is poor, (I have no idea how your equation works), but I may pick your brains about number theory sometime. I still have hopes of deciding the Twin Primes Conjecture one day.